Blindfold Nim

Memory limit: 32 MB

Sprague and Grundy have been playing the game called Nim. They put stacks of coins on the table and during the game they moved alternately. In each round a player would choose one stack and take any positive number of coins from it. The first player unable to make a valid move would lose.

Sprague and Grundy have quickly found the optimal strategy for this game and want to try something more interesting. They decided to play blindfold. This means all they know is that initially the number of coins in the 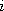-th stack is picked randomly from the range 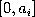, and the chance to pick any integer from this range is equal; the sizes of the stacks are determined independently. A player loses the game if he tries to take more coins from a stack than available. In particular, if the player knows that all the stacks are certainly empty, he is nonetheless forced to move and loses. Sprague is the first one to move. What is the probability of him winning, if we assume that both players play optimally and during the game they see each others' moves?

Input

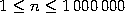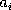In the first line of the standard input there is an integer (), denoting the number of stacks. The second line contains a sequence of positive integers . The sum of these integers does not exceed .

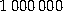Output

The first and only line of the standard output should consist of one real number - the probability that Sprague will win the game. The number printed can differ from the correct answer by no more than 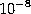. No more than 20 digits after the decimal point should be given.

Example

For the input data:

3
1 1 1

the correct result is:

0.375

Task author: Tomasz Idziaszek.